A Traveling Sinusoidal Wave Is Described by the Wave Function

Up to 256 cash back A sinusoidal wave on a string is described by die wave function y 015 sin 080x 50 t where x and y are in meters and t is in seconds. A What is the amplitude of the resultant wave function y y.

A Sinusoidal Wave Travelling In The Positive X Direction Has An Amplitude Of 15 0 Cm Youtube

Determine the-Speed of the wave.

. Engineering Electrical Engineering QA Library Two traveling sinusoidal waves are described by the wave functions y 475 sin a375x 1230t Y 475 sin 7375x 1230t 0250 where x y and y are in meters andt is in seconds. A traveling sinusoidal wave is described by the wave function y x t 0698 msin 693rt nx. Yxt A sinkx - ωt φ Here k is the wave number k 2πλ and ω 2πT 2πf is the angular frequency of the wave.

1 Answer to Two traveling sinusoidal waves are described by the wave functions y1 500 m sin p 400x - 1 200t And y2 500 m sin p 400x - 1 200t - 0250 Where x y1 and y2 are in meters and t is in seconds a What is the amplitude of the resultant wave. A sinusoidal wave is described by the wave function y 025 sin 030x 40t where x and y are in meters and t is in seconds. Two waves are traveling in the same medium and described by the following wave functions.

Two traveling sinusoidal waves are described by the wave functions y1 500m sinpie400x - 1 200t y2 500m sinpie400x - 1 200t -0250y where x y1 and y2 are in meters and t is in seconds. 35 times 12 is 420 centimeters per second. Problem 5 Easy Difficulty.

The displacement y of a particle in the medium is given as a function of x and t by. Determine the wavelength frequency and speed of the interfering waves. A What is the amplitude of the resultant wave function y1 y2.

26 Hz x and y are in meters and t is in seconds. The acceleration of gravity is 98. We have step-by-step solutions.

π 400 x 1200 t 0250 where x y 1 and y 2 are in meters and t is in seconds. Textbook solution for Physics for Scientists and Engineers. We want the wave Speed wave speed should equal wavelength times the frequency which is 35 centimeters times 12 hurts.

Um okay now we want to write an expression for the wave function. A What is the amplitude of the resultant wave function y_1y_2. A traveling sinusoidal wave is described by the wave function yx t 0564 msin607nt ax 5 6 where x and y are in meters and t is in seconds.

And now we want Uh huh. Recitation 3 Chapters 14 and 24 Problem 145. A traveling sinusoidal wave is described by the wave function y x t 0638 msin 690πt πx π 8 where x and y are in meters and t is in seconds.

Two sinusoidal waves travelling in opposite directions interfere to produce a standing wave described by the equation y 15 m sin 0400x cos 200 t where x is in metres and t is in seconds. Two traveling sinusoidal waves are described by the wave functions y1 485 sin 435x 1270t y2 485 sin 435x 1270t 0250 where x y1 and y2 are in meters and t is in seconds. Physics 06012021 0920 miyahvictoria.

Two traveling sinusoidal waves are described by the wave functionsy1 500 sin π400x 1 200ty2 500 sin π400x 1 200t 0250where x. Two traveling sinusoidal waves are described by the wave functions y 1 500 m sinˇ400x 1200t 1 and y 2 500 m sinˇ400x 1200t 0250 2 where x y 1 and y 2 are in meters and tis in secondsaWhat is the amplitude of the resultant wavebWhat is the frequency of the resultant wave. 94 Your response is within 10 of the correct value.

Two traveling sinusoidal waves are described by the wave functions beginarrayc y_1500 sin pi400 x-1200 t y_2500 sin pi400 x-1200 t-0250 endarray where x y_1 and y_2 are in meters and t is in seconds. A What is the amplitude of the resultant wave. Consider a transverse harmonic wave traveling in the positive x-direction.

A sinusoidal wave in a rope is described by the wave function y A sink x. So we got the angular frequency. Find the maximum transverse velocity of the element of the medium located at x 23 cm.

Y 1 500 m sin. Harmonic waves are sinusoidal waves. That would be in centimeters per second.

The mass per unit length of this string is 120 gm. A sinusoidal transverse wave that propagates in the positive x-direction can be described with the wave function y of xt is equal to A times cosine of start parenthesis k times x minus omega times t end parenthesis where k is the wave number x is the position of a point on the wave omega is the angular frequency and t is time. Where x and y are in meters and t is in seconds.

A sinusoidal wave traveling in the -x direction to the left has an ampli 0845 Two sinusoidal waves combining in a medium are described by the wave functio. Two traveling sinusoidal waves are described by the wave functions. T where A 047 m k 1 m1.

Determine for this wave a the amplitude b the angular frequency c the angular wave number d the wavelength e. Y 1 001 m sin 03 pi x-20t and y 2 001 m sin 03 pi x-20t where x and y are measured in centimeters and t is in seconds. Vibrator 26 Hz ì 38 gm m 188496 m If the tension in the rope is provided by an arrangement like the one illustrated above what is the value of the suspended mass.

B What is the frequency of the. M b What is the frequency of the wave. A traveling sinusoidal wave is described by the wave function - TTX 8 y x t 0616 msin 789nt where x and y are in meters and t is in seconds.

π 400 x 1200 t y 2 500 m sin. A What is the wavelength of the wave. Foundations and 1st Edition Katz Chapter 17 Problem 67PQ.

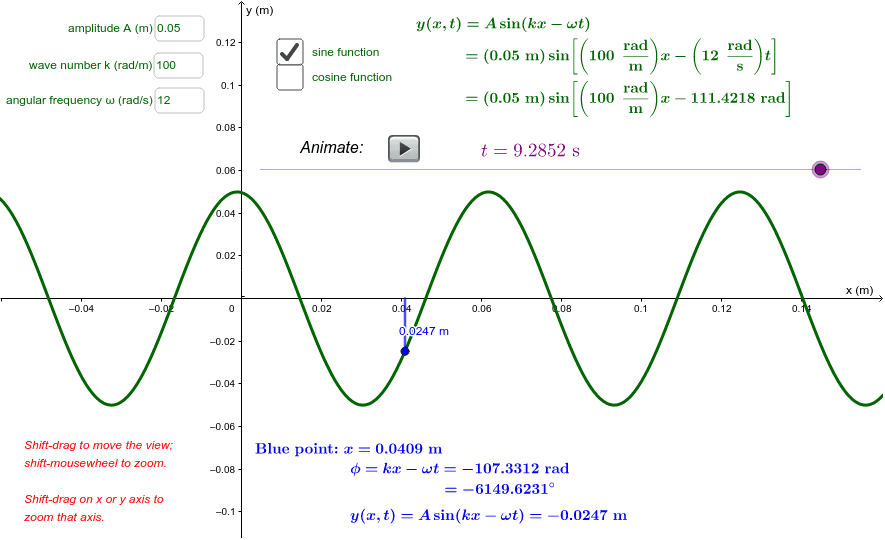
Traveling Wave Equation Geogebra

Wave Equation Wave Equation Waves Equation

Characteristics Of Sinusoidal Signals Sine Waves Video Tutorial